A l'heure actuelle, les réels R sont constitués par les entiers, les Rationnels, les Algébriques Réels et les Transcendants.
Les nombres les plus importants sont les nombres Transcendants car ils assurent la continuité de tout ce qui existe dans
l'Univers Visible.
On a vu que l'équation Un + Vn = an est impossible.
∀ n entier impair > 2 et ∀ U, V, a ∈ R tel que 1 ≤ U ≤ V ≤ a
On suppose u, v, a Transcendant, donc, un, vn, an Transcendants
On en déduit que la somme de 2 Transcendants qui sont des Réels n'est pas Réelle, donc pas Transcendante.
Donc, l'ensemble R n'est pas un groupe additif car l'addition n'est pas stable.
Donc, R n'est pas un corps.
Applications :
Les Mathématiciens ayant démontré qu'un des 2 nombres Réels π x e ou π + e est Transcendant.
π + e n'étant pas transcendant, on en déduit que π e est Transcendant.
On peut dire aussi : π + e ∉ R
π = 3.141... ... ... ... ... infinité de décimales non prévisibles
e = 2.718... ... ... ... ... infinité de décimales non prévisibles
On peut estimer que π + e est indéterminé car après avoir évacué le concept d'infini, on ne sait pas combien de décimales on prend.
On en déduit que les nombres transcendants sont fondamentalement indéterminés (en particulier π et e)
Ce qui a été évoqué sur les Transcendants est valable sur tous les autres nombres. Si on prend des concepts abstraits,
par exemple la Masse :
Ceci est valable sur n'importe quel concept que la physique élabore. On a le même problème sur les Algébriques :
La valeur √2 + √3 est indéterminée.
En résumé, on peut dire qu'un nombre avec une infinité de décimales n'a aucune réalité. On doit se soumettre à
la Logique constructiviste.
Tout ceci est en relation avec la propriété suivante :
Considérons un nombre transcendant α et l'extension transcendante Q(α)
Q(α) est isomorphe à Q(x)
Q(x) corps des fonctions rationnelles à une indéterminée x.
En conclusion, on peut dire que la Mathématique est fondamentalement indéterminée si on considère l'opérateur Addition.
1) Tout ce qui a été examiné précédemment confirme les relations d'incertitudes d'Heisenberg :
2) On comprend mieux l'inadéquation entre les intégrales fonctionnelles de R. Feynman qui divergent et le fait que ces mêmes intégrales arrivent à expliquer les interactions de particules élémentaires (Path Integrals).
Ceci est corrélé à la Réflexion du mathématicien R. Thom :
A ce niveau du développement, abordons le problème du désaccord entre A. Einstein et H. Bergson sur :
Pour la quasi totalité des scientifiques, le présent est un point de dimension nulle donc inaccessible.
On peut concevoir le présent d'une autre manière :
Le présent est un intervalle [a , b], intersection du passé et du futur.
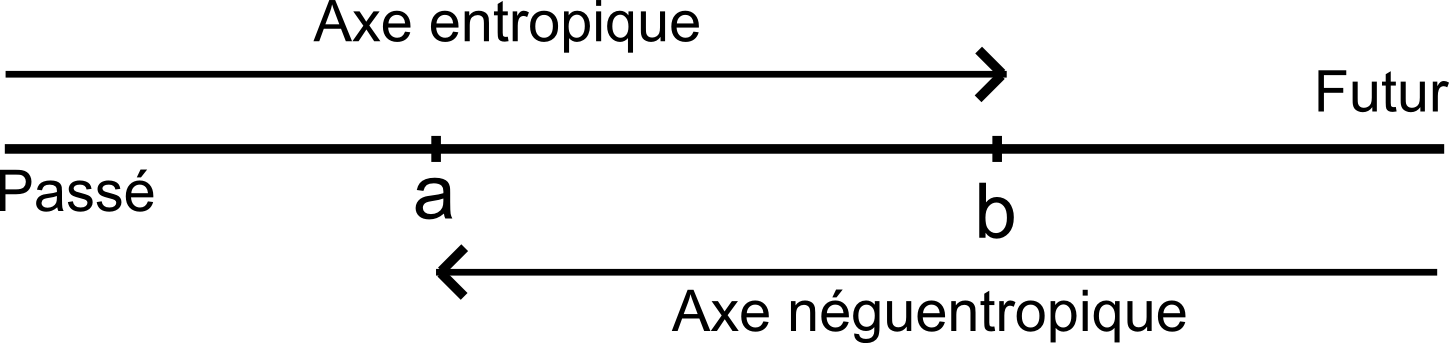
On a donc une Double causalité.
C'est la raison pour laquelle l'Antimatière remonte le temps sur [a , b].
C'est dans l'intervalle [a , b] que la Physique Quantique est opérationnelle.
De plus, ceci infirme un Big Bang global, malgré le décalage des raies spectrales vers le rouge (expansion) et
le fond cosmique à 2°.7
D'autre part, on explique facilement la Matière Noire. L'Information n'est pas encore arrivée sur Terre.
On a donc le principe "l'Information vient du Futur"
Il serait peut-être judicieux de réexaminer la démarche de L'astrophysicien F. Hoyle.
Passons en Mécanique analytique et en Mécanique Céleste avec le problème à 3 corps
Ce problème a été étudié par les Mathématiciens Clairaut, Euler, Lagrange, ... puis plus tard par H. Poincaré, ... (Les outils Mathématiques sont le Lagrangien, l'Hamiltonien, ...)
On n'a pas pu résoudre analytiquement ce problème dans tous les cas, car la somme et la différence de 2 Réels est indéterminée.
Abordons maintenant les problèmes Cosmologiques (Modèles d'Univers proposés depuis la Relativité générale).
La Courbure de l'Univers (Hyperbolique, Elliptique, ...) s'explique par le fait que les Réels ne sont pas sur une Droite.
Tous les résultats précédents confirment "la Gravitation quantique à boucles" (Ashtekar, Smolin, Rovelli, ...)
Dans cette théorie, il n'y a pas de repère et d'origine. On a évacué le concept d'Infini.
L'Univers est un Graphe (Espace - temps) composé de "Quantums d'Espace Temps" (L'Infiniment grand est quantique).
Il suffit d'expliquer comment les Quantums d'Espace Temps se recollent suivant la zone d'Univers. Il faut bien entendu confirmer par des preuves expérimentales.
En conclusion, contrairement à ce qu'a pu dire D. Hilbert en 1900 :
NB :
1) Sur le plan philosophique, il faut adopter la démarche de Pythagore, Platon, Fermat, Pascal, Leibniz, Poincaré, ...
2) Les Distances de tous les objets de l'Univers (Galaxies, Trous noirs, Pulsars, Quasars, ...) ainsi que les Datations de tous les événements sont inexactes.


