 |
||
  |
L'équation 
Un + Vn = an est impossible ∀ U, V, a ∈ R tel que 1 ≤ U ≤ V ≤ a et ∀ n > 2 n entier impair.
Dans un repère orthonormé ( ou , ov ) la représentation graphique de l'équation est une courbe ( Γn ) comprise entre
le cercle ( C ) U² + V² = a² et le carré K de côté a.
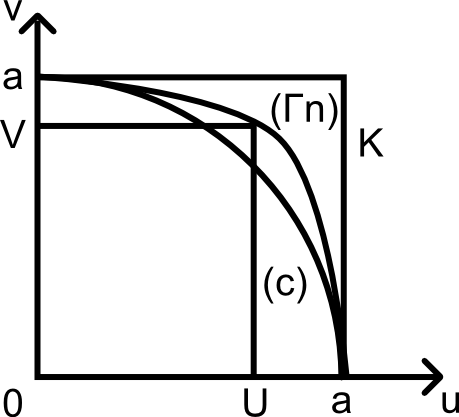
On a forcément U ≤ V < a < U + V.
Passons en géométrie élémentaire.
Considérons un triangle PQR tel que :
- PQ = U
- QR = V
- PR = a
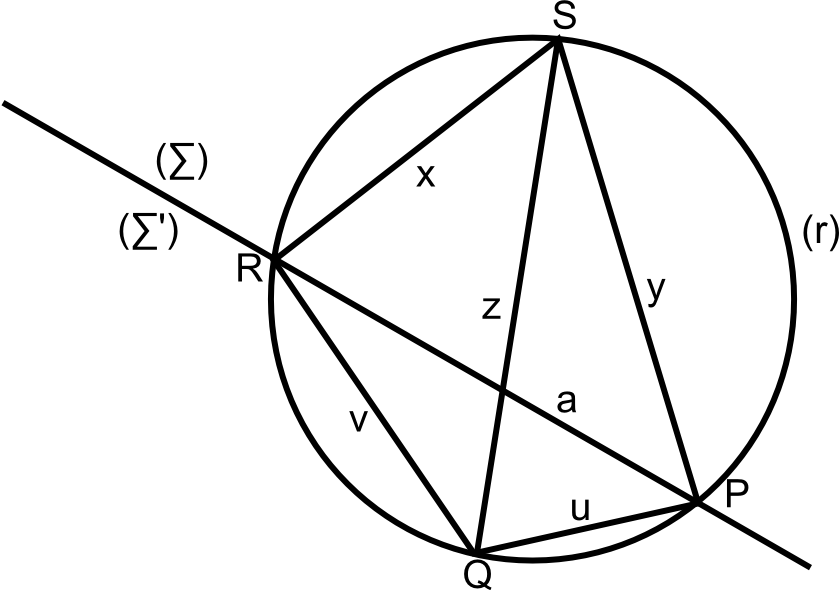
Considérons un quadrilatère PQRS tel que :
- SR = x
- SP = y
- SQ = z
Avec la condition 
x < y < z
la droite (PR) partage le plan en 2 régions (∑) et (∑')
Avec la condition le point S ∈ (∑)
Donc, le quadrilatère PQRS est convexe.
D'autre part, on a :
- Un = (a - V) A avec A = an-1 + an-2 V + ......... + a Vn-2 + Vn-1
- Vn = (a - U) B avec B = an-1 + an-2 U + ......... + a Un-2 + Un-1
- an = (U + V) C avec C = Un-1 - Un-2 V + ......... - U Vn-2 + Vn-1
On en déduit : (U + V) C = (a - V) A + (a - U) B
Donc a (A + B) = U (B + C) + V (A + C) 
On constate qu'on a C < B < A
On en déduit : B + C < A + C < A + B
En posant :
- x = B + C
- y = A + C
- z = A + B
La condition précédente est vérifiée.
On a donc :
az = Ux + Vy
D'après la réciproque du Théorème de PTOLÉMÉE
Si le quadrilatère PQRS existe, alors le quadrilatère PQRS convexe est inscriptible dans le cercle (Γ) circonscrit au triangle PQR.
Dans le triangle PQS, d'après l'inégalité triangulaire, on doit avoir :
C'est à dire : A + B < A + C + U
D'où B - C < U
Or : B - C = an-1 - Vn-1 + U (an-2 + Vn-2) + ...... + Un-2 (a + V) > U
Car 1 ≤ U ≤ V < a
On arrive donc à une contradiction.
On en déduit que le quadrilatère PQRS n'existe pas car le point S n'existe pas.
Le point S n'existe pas car les trois triangles SRQ, SPQ, SRP n'existent pas. En effet, une des trois inégalités triangulaires n'est pas vérifiée.
Un petit calcul montre que :
z > V + x
z > U + y
Donc, le point S n'existe pas à cause des expressions de x, y, z qui sont des fonctions de A, B, C qui sont directement liées au fait que :
Un+Vn = an.
On en déduit un résultat surprenant.
Dans un triangle PQR :
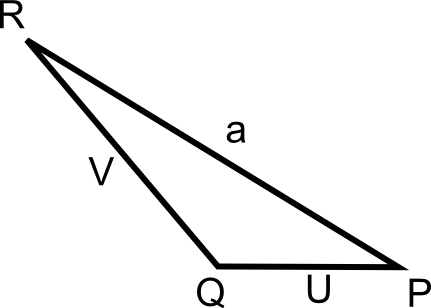
Pour n impair l'égalité Un + Vn = an est impossible sur les réels.
On en déduit que la courbe ( Γn ) n'existe pas.
Le dernier Théorème de FERMAT est donc démontré pour les entiers.
- 1) Si on admet avec DEDEKIND que tous les nombres Réels sont sur une Droite ( N , Z , Q , Algébriques Réels , Trancendants ), R est totalement ordonné.
Considérons a, U algébriques Réels
Donc V = n√(an - Un) algébrique Réel
On en déduit le résultat :
Les algébriques n√ pour n impair n'appartiennent pas à la droite Réelle R.
On en déduit que R n'est plus totalement ordonné.
- 2) On comprend mieux la Théorie de GALOIS : Les solutions des équations de degré ≥ 5 ne peuvent pas s'exprimer avec des formules (ou des signes - radicaux).
- 3) La Duplication du Cube est impossible : 3√2 est non constructible.
On voit se profiler le problème de la logique constructiviste par rapport à la réalité de l'Univers.
- 4) Abordons les nombres Transcendants ( π , e , ......). On a montré Un + Vn = an impossible pour U, V, a Réel ≥ 1.
On peut prendre U = π transcendant, V et a Réels
Ceci explique pourquoi on ne peut pas exprimer par une Formule ( Série entières, ......) π3 , π5 , π7 , ......, alors que c'est possible pour π2 , π4 , π6 , ......
- 5) Ce résultat est à rapprocher de l'étude des infiniments petits de LEIBNIZ par l'Analyse non standard de ROBINSON.
On a vu que l'équation Réelle de FERMAT Un + Vn = an est impossible pour n impair ( n > 2 ) et pour U, V, a ∈ R tel que :
1 ≤ U ≤ V < a < U + V
Transposons sur le plan géométique :
Soit un triangle ABC tel que :
- AB = U
- AC = V
- BC = a
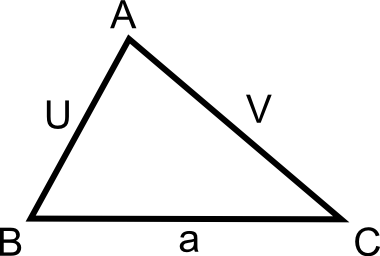
Les côtés du Triangle [AB] , [AC] , [BC] sont des segments de Droite représentés par des Réels U , V , a. Or, d'après DEDEKIND, il y a correspondance bijective entre les Réels R et les points d'une Droite munie d'une origine o et d'une unité 
.
R ( N , Z , Q , A algébriques réels, T transcendants).
L'équation de FERMAT est impossible pour les Réels supérieurs à 1. (On a 3 réels U , V , a représentés par les segments de droite [AB] , [AC] , [BC]).
Tout ceci revient à dire que dans un triangle ABC ( U , V , a ) on ne peut pas avoir Un + Vn = an (n impair > 2).
A présent, passons au système orthonormé de coordonnées ( ou , ov ) (DESCARTES). ( ou ) et ( ov ) sont 2 Droites Réelles d'après DEDEKIND.
La représentation géométrique de l'équation Un + Vn = an est une courbe (Γn) comprise entre le cerle ( C ) U² + V² = a² et le carré K de côté a.
Si on suppose avec DEDEKIND que les réels a, U sont sur l'axe ( ou ), alors le réel V ∈ ( ov ) mais V ∉ ( ou )
On peut dire aussi :
2 points A et B déterminent une Droite ( D )
Si on considère sur ( D ) une origine o et une unité .
Alors aux points A et B correspondent 2 réels a et b ( a et b > 1 )
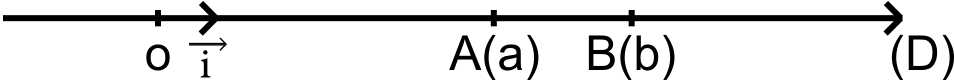
Soit c ∈ R c ≠ a, b
Soit le point C correspondant à c ( c > 1 )
Alors C ∉ (D)
On en déduit un résultat gigantesque :
Les Réels R supérieurs à 1 ne correspondent pas aux points d'une Droite ( o , )
Cas particulier : Les entiers N ( 1, 2, 3, ...) ne sont pas alignés sur une Droite. Il en est de même pour les premiers ( 1, 2, 3, 5, 7, ...)
Considérons la Fonction ζ de RIEMANN :
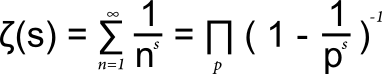
On sait que :
- ζ (2n) transcendants ∀ n
- ζ (2n + 1) irrationnels pour une inf inité de n
La conjecture de RIEMANN nous dit :
En posant s = σ + i t, les zéros de la Fonction ζ sont situés sur la Droite σ = 1/2 dans la Bande critique 0 < σ < 1
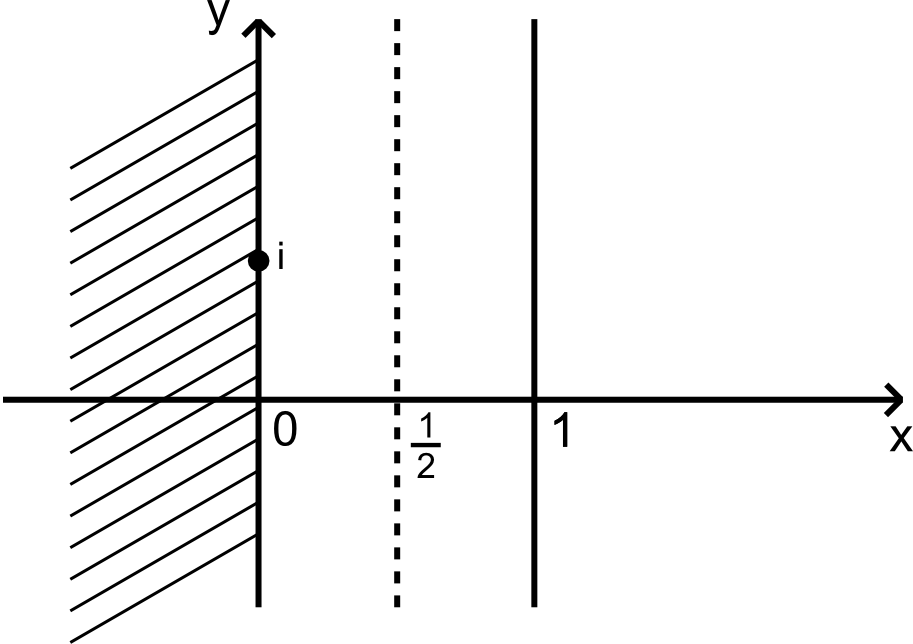
Les Mathématiciens n'arrivent pas à démontrer cette conjecture (vérifiée le plus loin possible par ordinateur) parce que la Droite réelle n'existe pas. On en déduit que le concept d'Infini n'est pas corrélé "au bout de la droite".
Ici se pose le problème de l'Ordinateur :
Un ordinateur est une machine linéaire (il ne connaît pas la courbe ; il l'approche par ses tangentes).
Un ordinateur, aussi puissant soit-il, ne pourra jamais accéder aux possibilitées de l'Esprit Humain (La Conscience Universelle).
On en déduit que l'Intelligence artificielle n'accèdera jamais à la Puissance de l'ESPRIT car ce dernier est non linéaire.
Poursuivons notre réflexion sur l'équation Réelle de FERMAT Un + Vn = an
On a vu que l'équation est impossible pour U, V, a réels supérieurs à 1, et n > 1 avec n impair.
L'équation est une courbe ( Γn ) comprise entre le cercle ( C ) U² + V² = a² et le carré K de côté a.
Il faut préciser que l'équation est impossible pour U, V, a ∈ R
Simultanément
Donc U, a ∈ R sur (ou) Droite Réelle
On n'a pas le droit de rabattre V avec le cercle sur ( ou )
De même V, a ∈ R sur ( ov ) Droite Réelle
REMARQUE : Antérieurement les Mathématiciens ont rabattu √2 sur ( ou ).
En ( √2, 0 ) mais n'ont pas rabattu i sur ( ou ) en ( 1,0 ), sinon, l'ensemble des nombres complexes C n'existerait pas.
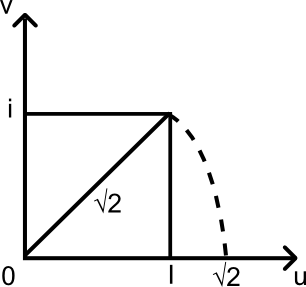
C a permis une compréhension très vaste de certaines branches de la Mathématique.
On en conclut :
En prenant une origine o ∈ ( D ) et une unité 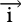sur ( D ) (||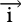|| = 1)
Aux points A et B correspondent les réels a et b
Soit c ∈ R ; c ≠ a , b alors le point C ( c ) ∉ ( D ). En appliquant ce principe aux points A ( 1 ) et B ( 2 ) appartenant à ( Ax )
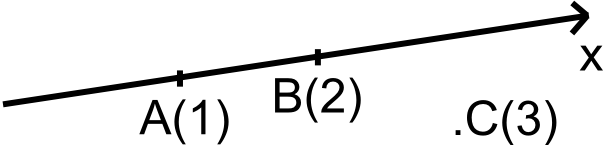
L'unité de mesure ne peut pas se reproduire. C ( 3 ) ∉ ( Ax )
On en déduit le principe suivant : "Les nombres entiers servent à dénombrer mais ne peuvent pas servir à mesurer des quantités quelque soient les variables employées"
Toutes les Sciences sont atteintes par ce résultat.
Inversement, si on applique le principe à 2 points A ( a ) et B ( b ) auxquels on a attribués 2 valeurs arbitraires a et b tel que 1 ≤ a < b on ne sait pas où se trouve l'origine O ( o ) !!!
Abordons quelques problèmes généraux sur le fonctionnement de la SCIENCE.
D'après le théorème d'incomplétude de GODEL, "une propriété peut être vraie mais indémontrable", on peut ajouter un autre principe :
Il faut sortir de la Logique Aristotélicienne (Logique du tiers exclu) pour entrer dans la Logique Non-Aristotélicienne
(Logique du tiers inclus), on peut, à présent, proposer les 2 principes suivants :
- Une propriété peut être à la fois "non Vrai et non Fausse" tant qu'elle n'a pas été expérimenté dans l'instant (Physique Quantique)
- Tout système d'Axiomes fini aboutit au bout d'un certain temps à ses propres contradictions.
Abordons quelques problèmes epistémologiques et psychanalytiques :
-
Dans l'Inconscient collectif terrestre, on comprend mieux la démarche de LEIBNIZ qui voulait démontrer que 1 + 1 = 2
Signalons au passage qu'en Relativité Restreinte 1 + 1 = 1 (c vitesse de la lumière)
ou 1 + 1 = 1,99... (ΔE = Δm.c²)
1 atome + 1 atome = 2 atomes
1m + 1m = ???? (m, mètre)
L'unité de mesure ne se reproduit pas.
-
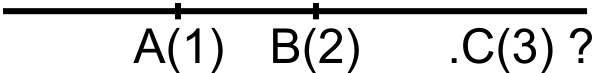
L'impossibilité de la quadrature du Cercle démontré par LINDEMANN
"π n'est pas solution d'une équation algébrique, π transcendant"
Provoque la réaction de KRONECKER suivante :
"Cela ne m'intéresse pas car π n'existe pas"
-
Une réflexion de BOREL sur le nombre π
"Les décimales de π varient suivant le point d'Univers"
Pour conclure, abordons quelques problèmes Métaphysiques et Sémiologiques
Il semble que la Distance entre la Vérité et la Réalité est colossale, voire infinie.
Enfin, on peut remettre en question l'Universalité de la Mathématique Terrestre.
Approfondissons les conséquences de l'équation réelle de FERMAT.
Soit l'équation Un + Vn = an avec U, V, a ∈ R, et n impair.
Cette équation est impossible pour U, V, a > 1
Considérons les extensions successives de Q :
E = Q(√p1, ..., √pn) est un espace vectoriel de dimension 2n sur Q
Prenons ω Puissance du Dénombrable
2ω Puissance du Continu
On a E ⊂ AR ⊂ A
Soit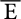 
= Q(√p1, √p2, ..., √pn, ...)
Card (P) = ω
Donc 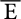est un espace vectoriel de dimension 2ω sur Q. Donc card(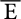) = ω(2ω) = (2ω)
Or E ⊂ 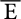⊂ AR ⊂ A avec card A = ω d'après CANTOR, on arrive à une absurdité
2ω < ω
Donc AR ⊄ R
Revenons à notre équation de Fermat :
Considérons a, U ∈ (D) ⊂ E sur (ou) avec (D) nombres constructibles (Wantzel)
V = n√(an - Un) ∉ (D)
On ne peut pas rabattre V sur (o,u) avec le compas
V ∉ R (Droite réelle de Dedekind)
Le concept même de constructibilité est à revoir.
On peut proposer les réflexions suivantes :
Les nombres entiers, rationnels, algébriques réels en tant que signifants symboliques n'ont pas de signifiants géométriques car ils sont de mesure nulle.
Il apparait aussi que R n'a pas la puissance du continu 2ω si on veut que AR ⊂ R
On a considéré 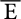= Q (√p1, √p2, ..., √pn, ...)
On peut continuer le processus
En considérant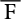 
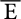= (3√p1, 3√p2, ..., 3√pn, ...) avec 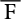espace vectoriel de dimension 2ω sur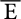
Or card(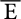) = 2ω
Donc card(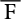) = (2ω)(2ω)
Remarques : Les deux principes suivants sont inadaptés
∀ x1, x2 ∈ Q rationnels avec x1 < x2
∃ r ∈ R tel que x1 < r < x2 impossible
∀ r1, r2 ∈ R ∃ x ∈ Q tel que r1 < x < r2 impossible.
On en déduit que Q n'est plus dense dans R
Abordons à présent les nombres premiers (P)
Card (P) = ω et card N = ω
(P) ⊂ N
N n'est pas le plus petit ensemble dénombrable
Considérons :
(P1) = {p1, p12, ...,p1n, ...}
(P2) = {p2, p22, ...,p2n, ...}
... ... ...
(Pk) = {pk, pk2, ...,pkn, ...}
... ... ...
Card (Pi) = ω ∀ i = 1, 2, ..., k, ...
p1 = 2, p2 = 3, p3 = 5, p4 = 7, ... etc
N est l'ensemble de toutes les combinaisons possibles
On choisi un élement, et un seul, dans chaque (Pi)
( La décomposition en facteurs premiers d'un nombre entier est unique )
Donc card N = 2ω
N a la puissance du Continu (on ne peut pas compter des objets, des points, des signes, ... de mesure nulle.)
Il n'existe aucune bijection de (P) sur (N) ( le signifiant continu est inadapté )
On peut envisager que :
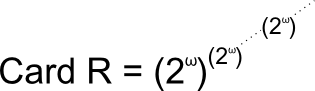Transfinis de CANTOROn peut envisager que les nombres premiers soient les archétypes fondamentaux de l'Univers.
Réflexions sur les Nombres :
Les Nombres entiers, rationnels, algébriques sont de mesure nulle. Ils sont donc non localisables sur le plan géométrique car ils n'ont pas de signifiants. Ils appartiennent à l'Invisible. Le paradoxe est le fait que ce soit les nombres les mieux appréhendés sur le plan intellectuel par les Mathématiciens. Par contre, les nombres Transcendants qui participent à la cohésion et à l'existence même de tout objet visible sont très difficile à étudier. Ces propos sont en relation avec le problème de la reproduction de l'unité de mesure pour les entiers quand on sait que la Série Harmonique diverge quelque soit le terme où on démarre la sommation.
Le fait que AR ⊄ R ( Droite Réelle ) AR ( algébrique Réels )
A cause des n√ n impair, va dans le même sens que le Théorème de LIOUVILLE.
"L'approximation des Transcendants par des Rationnels est bien meilleure que celle des nombres algébriques".
Les Espaces R, R², R³, ... , Rn ne sont que des Représentations.
Comme le dit le grand Mathématicien Henri POINCARE :
"L'Espace R³ ( ox, oy, oz ) n'est qu'une représentation de l'Espace Réel. Il y a peut-être une distance importante entre la Réalité et l'idée qu'on s'en fait.
