The equation Un + Vn = an is impossible ∀ U, V, a ∈ R with 1 ≤ U ≤ V ≤ a and ∀ n > 2        n odd integer.

In the orthonormal system ( ou , ov ) the graphical representation of the equation is a curve ( Γn ) in between
the circle ( C ) U² + V² = a² and the square K of side a.

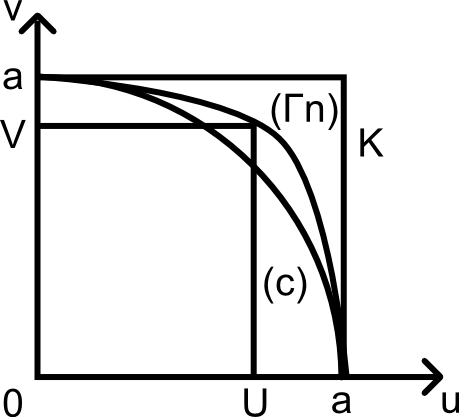
Inevitably we have U ≤ V < a < U + V.


Let us pass on to elementary geometry.

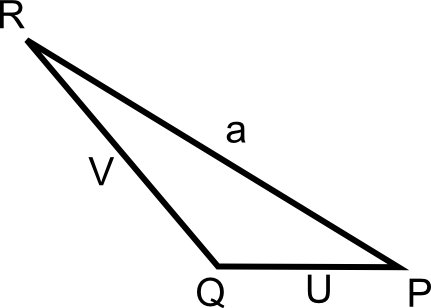
Let us consider a triangle PQR with :

  • PQ = U
  • QR = V
  • PR = a

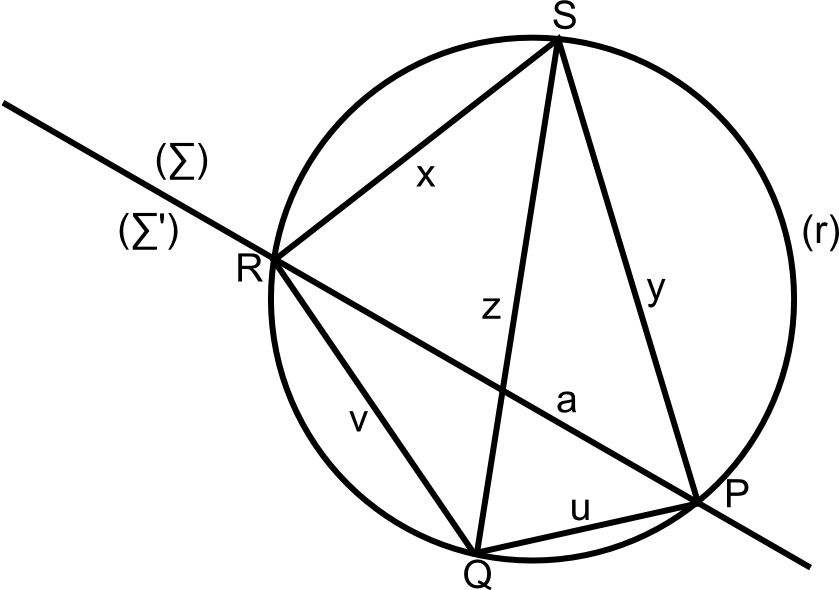
Let us consider a quadrilateral PQRS with :

  • SR = x
  • SP = y
  • SQ = z

With the condition x < y < z

The straight line (PR) divides the graph into 2 domains (∑) and (∑')

With the condition the point S ∈ (∑)

Thus, the quadrilateral PQRS is convex.


On the other hand, we have :

  • Un = (a - V) A avec A = an-1 + an-2 V + ......... + a Vn-2 + Vn-1
  • Vn = (a - U) B avec B = an-1 + an-2 U + ......... + a Un-2 + Un-1
  • an = (U + V) C avec C = Un-1 - Un-2 V + ......... - U Vn-2 + Vn-1

We can deduce : (U + V) C = (a - V) A + (a - U) B

Thus a (A + B) = U (B + C) + V (A + C)


It is found that we have C < B < A

We can deduce : B + C < A + C < A + B

With :

  • x = B + C
  • y = A + C
  • z = A + B

The alove condition is satisfied.

So we have :

az = Ux + Vy

According to the reciprocal of the PTOLEME theorem

If the quadrilateral PQRS exists, then the quadrilateral PQRS convexe est inscriptable in the circle (Γ) circonscribed to the triangle PQR.


in the triangle PQS, based in the triangular inequality, we must have :

z < y + U

That is to say : A + B < A + C + U

Thus B - C < U

Now : B - C = an-1 - Vn-1 + U (an-2 + Vn-2) + ...... + Un-2 (a + V) > U

Because 1 ≤ U ≤ V < a


Thus we arrive to the contradiction.

It can be deduced that the quadrilateral PQRS does not exist since the point S does not exist.

The point    S   does not exist since the three triangles SRQ, SPQ, SRP do not exist. Indeed, one of the three triangular inequality is not verified.

A little calculation shows that :

z > V + x
z > U + y

Therefore, the point   S   does not exist because of the expression of x, y, z which are fonctions of A, B, C which are directly related to the fact that :

Un+Vn = an.


Thus a surprising result can be deduced.

In the triangle PQR :

For n odd the equality Un + Vn = an is impossible for real numbers.

1 ≤ U ≤ V < a

This, the Fermat's last Theorem is proved for integers.